Guangyang Zeng

Guangyang Zeng

Postdoctoral Fellow

Projects

Low-complexity Distributed Detection with One-bit Memory Under Neyman-Pearson Criterion

drawing

Distributed detection, which arose from multi-radar object detection, has gained its flourishing with the development of wireless sensor networks (WSNs). It is now widely applied in WSNs-based event detection, e.g., spectral sensing in cognitive radio networks, distributed intrusion detection systems, and distributed detection of human activities.
In this project, we consider a multi-stage distributed detection scenario, where n sensors and a fusion center are deployed to accomplish a binary hypothesis test. At each time stage, local sensors generate binary messages and then upload them to the FC for global detection decision making. We suppose a one-bit memory is available at the FC to store its decision history and focus on developing iterative fusion schemes. We first visit the detection problem of performing the Neyman-Pearson test at each stage and give an optimal algorithm, called the oracle algorithm, to solve it. Noticing the computational inefficiency of the oracle fusion, we then propose a low-complexity alternative, for which the likelihood ratio test threshold is tuned in connection to the fusion decision history compressed in the one-bit memory. The low-complexity algorithm greatly brings down the computational complexity at each stage from O(4^n ) (worst case) to O(n). We show that two algorithms exponentially converge to the same performance with the increase of time stages. In addition, the rates of convergence are proven to be asymptotically identical. The proposed low-complexity algorithm is applied in real experiments of done detection using multiple acoustic sensors. Experiment results show that the one-bit information can effectively improve detection performances.

Localizability with Range-Difference Measurements: Numerical Computation and Error Bound Analysis [MATLAB Code]

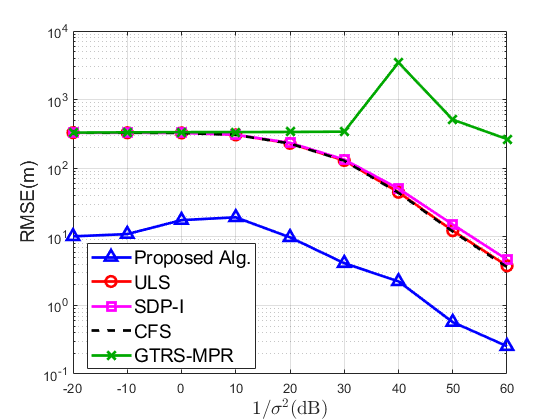
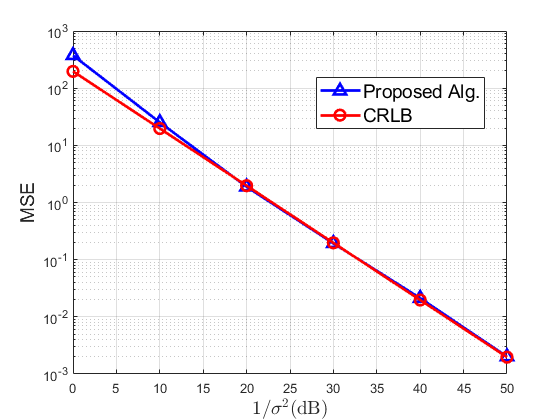
In this project, we study the source localization problem based on range-difference measurements, or equivalently time difference of arrival (TDOA) measurements. TDOA is a high-precision localization technique and has various applications, ranging from the global positioning system, cellular network localization to under-water sonar positioning. In TDOA-based localization, there is a reference sensor, and for each other sensor, the TDOA measurement is obtained with respect to the reference one. By minimizing the sum of spherical least squares errors, a nonconvex constrained least squares (CLS) problem is constructed. To the best of our knowledge, there is no literature giving a complete algorithm to calculate the global minimizer of this CLS problem. We first derive a set of theoretical results on the existence of a global solution and its explicit characterizations. We then develop an efficient algorithm to solve the CLS problem based on our theoretical findings. We also propose guidelines on sensor deployment to improve localization accuracy. Simulation and real-world experiments in our system demonstrate significant localization error drop compared with existing algorithms.

drawing drawing

Global and Asymptotically Efficient Localization from Range Measurements [MATLAB Code]

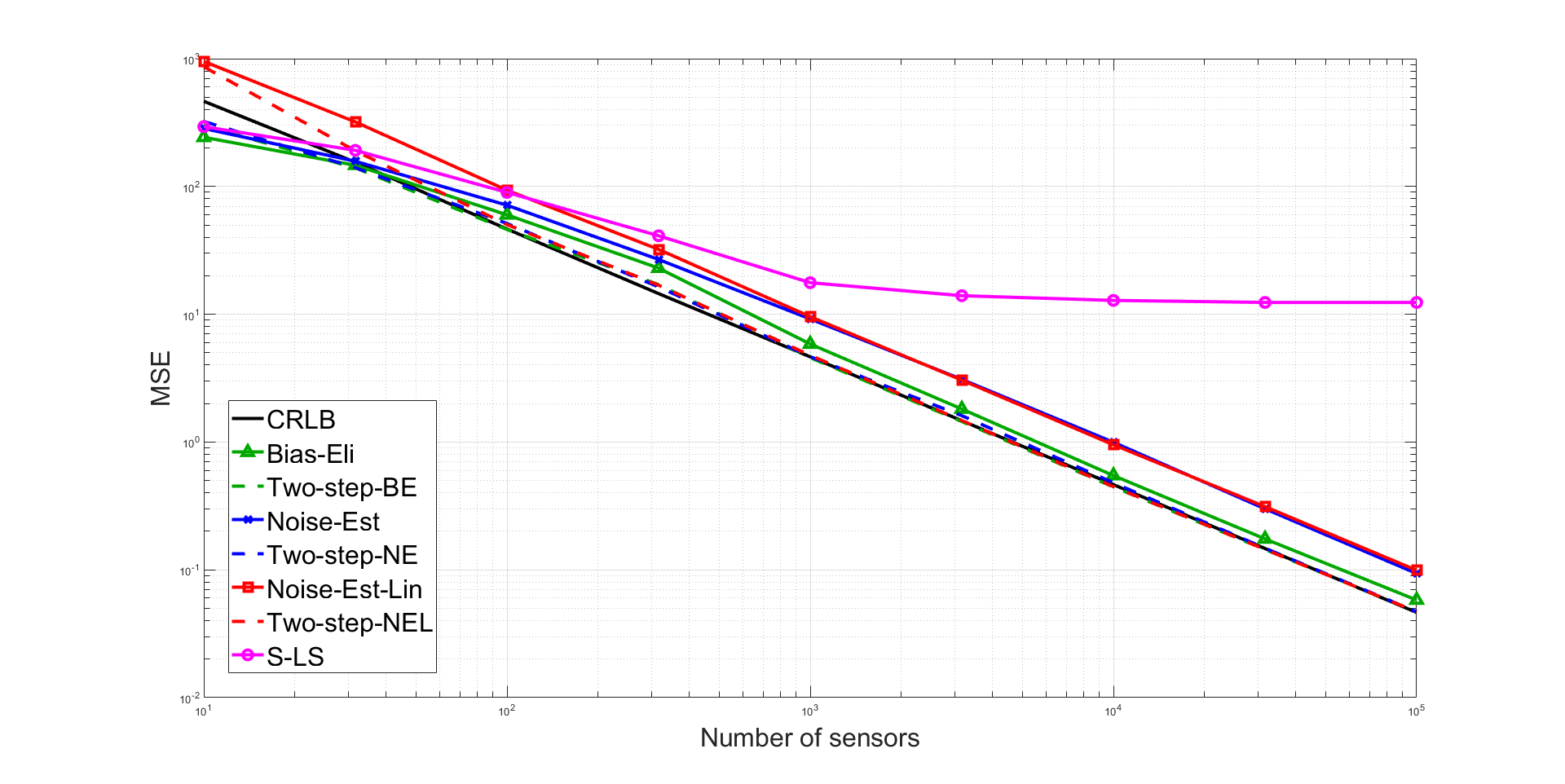
In this project, we consider the range-based localization problem, which involves estimating an object’s position by using $m$ sensors, hoping that as the number $m$ of sensors increases, the estimate converges to the true position with the minimum variance. We show that under some conditions on the sensor deployment and measurement noises, the LS estimator is strongly consistent and asymptotically normal. However, the LS problem is nonsmooth and nonconvex, and therefore hard to solve. We then devise realizable estimators that possess the same asymptotic properties as the LS one. These estimators are based on a two-step estimation architecture, which says that any $\sqrt{m}$-consistent estimate followed by a one-step Gauss-Newton iteration can yield a solution that possesses the same asymptotic property as the LS one. The keypoint of the two-step scheme is to construct a $\sqrt{m}$-consistent estimate in the first step. In terms of whether the variance of measurement noises is known or not, we propose the Bias-Eli estimator (which involves solving a generalized trust region subproblem) and the Noise-Est estimator (which is obtained by solving a convex problem), respectively. Both of them are proved to be $\sqrt{m}$-consistent. Moreover, we show that by discarding the constraints in the above two optimization problems, the resulting closed-form estimators (called Bias-Eli-Lin and Noise-Est-Lin) are also $\sqrt{m}$-consistent. Plenty of simulations verify the correctness of our theoretical claims, showing that the proposed two-step estimators can asymptotically achieve the Cramer-Rao lower bound.

drawing